Вишедимензионални низ – дефиниција

Хајде да искористимо оно што смо досад научили. Креирајмо и иницијализујмо три једнодимензионална низа a, b, c са по пет целих бројева:

int a[5] = {1, 2, 3, 4, 5};
int b[5] = {6, 7, 8, 9, 10};
int c[5] = {11, 12, 13, 14, 15};

Да видимо шта се дешава у меморији.

Добили смо један нови низ који се састоји од три низа који су у меморији поређани један за другим. Да видимо како можемо направити једну нову променљиву којом би приказали сва три низа.

Посматрајмо ово мало другачије. Можемо низове да поставимо један испод другог у виду табеле и да сваки означимо новим индексом. Назовимо ту нову променљиву А и доделимо сваком реду индекс.

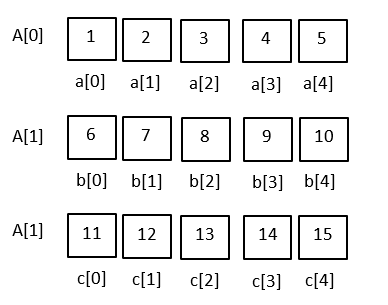
У математици овакав распоред се назива матрица. Матрица има свој ред (врсту) и своју колону.

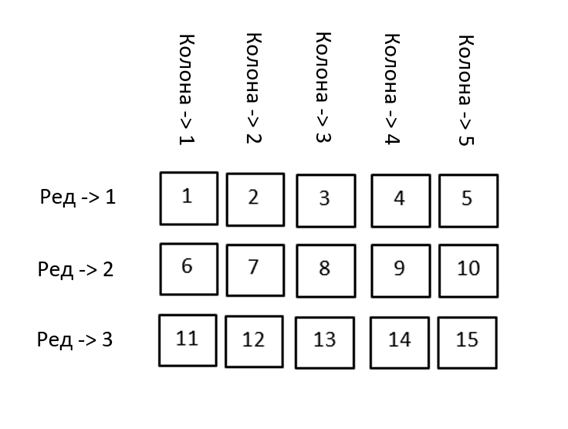
Хајде да елементима матрица А доделимо одговарајуће индексе и представимо их математички.

Шта примећујете? Као и код једнодимензионалног низа, индекси почињу од нуле. Овде имамо два индекса. Први индекс означава индекс реда, а други индекс колоне. Значи, ако за индекс реда уведемо променљиву \(i\), а за индекс колоне \(j\), добићемо општи члан матрице \(А_{ij}\).

С обзиром да у коду нисмо у могућности да на овај начин напишемо индексе, послужићемо се синтаксом једнодимензионалног низа и додаћемо још једну угласту заграду. Ако уз сваки индекс реда додамо индекс колоне у којој се елеменат налази, долазимо до тога да сваки елемент има у себи два индекса: индекс реда и индекс колоне А[red][kolona].

Долазимо до израза A[i][j].

У меморији су они сада смештени и означени на следећи начин:

Као и код једнодимензионалног низа, и овде морамо унапред резервисати меморијски простор за смештање елемената низа. Тако долазимо до синтаксе за дефинисање матрице.

tip_elemenata ime_niza [br_redova][br_kolona];

Дефинисати матрицу B која садржи целе бројеве и има 3 реда и 4 колоне.

Решење: int B[3][4];

Задатак: Дефинисати матрицу C која садржи податке типа double и има 5 редова и 4 колоне.

Решење: double C[5][4];

Питање: Колико највише елемената може да се смести у низ A[5][12]?

Решење: Максималан број елемената је 60.

Хајде да уопштимо. Нека број редова буде r, а број колона k.

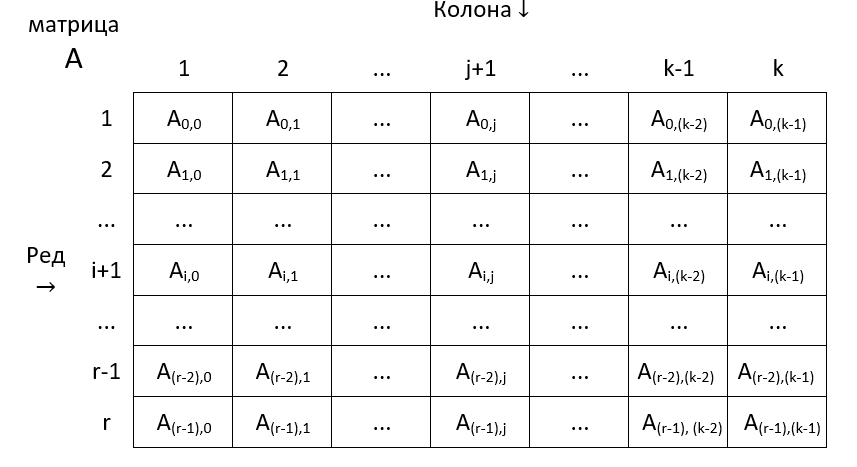
Шта примећујеш? Последњи индекс реда је r-1, а колоне k-1.

Ово је јако битно јер се увек даје број редова и колона, а индекси почињу увек од нуле.

Посматрајмо ово као лист папира и додајмо још једну димензију која ће престављати број листа (слоја).

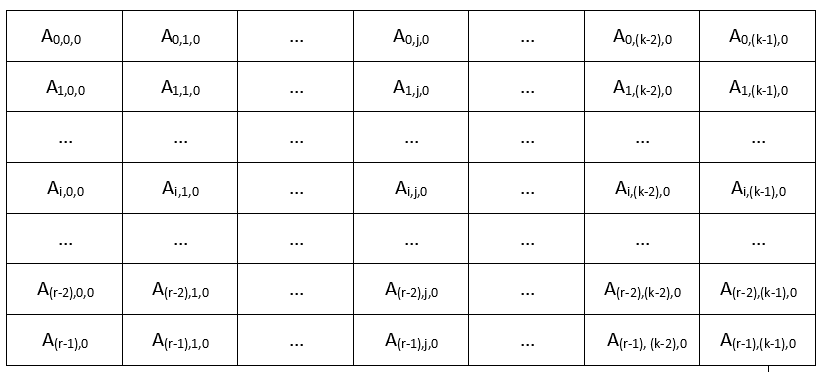
Направимо још један овакав лист тако што ћемо индекс листа означити са један.

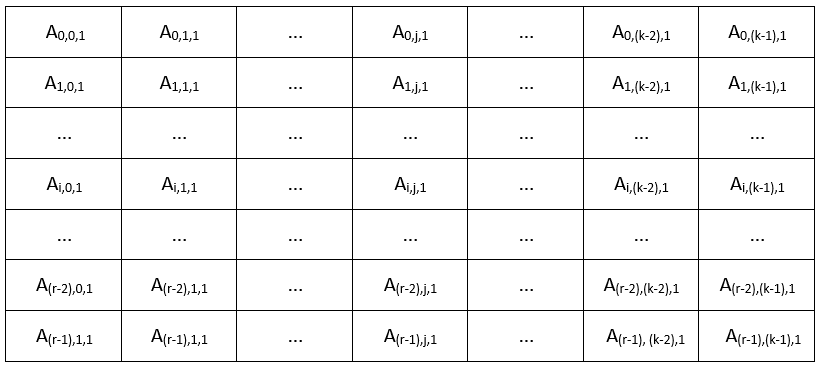
Направимо l-ти овакав лист и поставимо их један иза другог.

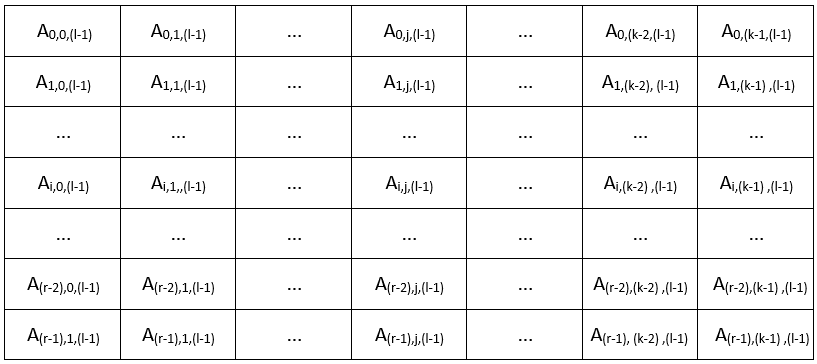
На овај начин добили смо један тродимензионални низ који се састоји из одређеног броја редова, колона и листова (слојева) и код кога је сваки елемент дефинисан са три индекса.

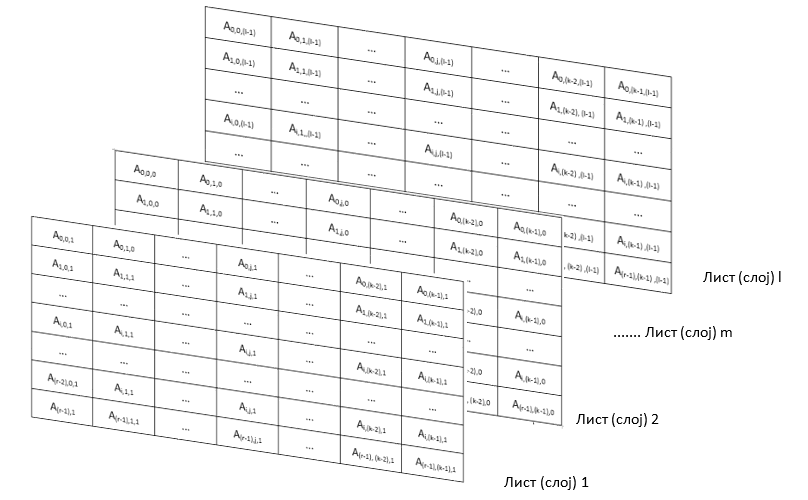
Долазимо до дефиниције тродимензионалног низа:

tip_elemenata ime_niza [br_redova][br_kolona][br_slojeva];

Дефинисати тродимензионални низ B који садржи целе бројеве и има 3 реда, 3 колоне и 3 листа (слоја).

Решење: int B[3][3][3];

Дефинисати тродимензионални низ C који садржи податке типа double и има 5 редова, 4 колоне и 2 листа (слоја).

Решење: double C[5][4][2];

Колико највише елемената може да се смести у низ A[5][12][5]?

Решење: Максималан број елемената је 300.

Навести један карактеристичан предмет који се може назвати тродимензионалним низом.

Решење: Рубикова (мађарска) коцка.

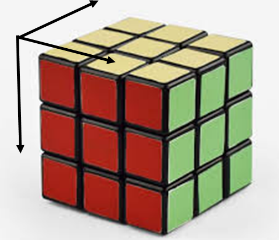
Математички можемо додати четврту, пету, шесту… n-ту димензију, али то је домен више математике.

Долазимо до дефиниције n-димензионалног низа:

tip_elemenata ime_niza [br_dimenziје_1][br_dimenziје_2][ br_dimenziје_3].....[ br_dimenziје_n];

Ми даље настављамо да анализирамо дводимензионални низ (матрицу). Ако научите како се ради са матрицама, научићете да радите и са низом од било колико димензија.